
Archimedes of Syracuse (c.287 BC - c. 212 BC) was an ancient Greek mathematician, physicist and engineer. Although little is known about his life, he is regarded as one of the most important scientists in classical antiquity. In addition to making important discoveries in the field of mathematics and geometry, he is credited with producing machines that were well ahead of their time.
The Ancient Roman historians showed a strong interest in Archimedes and wrote several biographies relating to his life and works, while the few copies of his treatises that survived through the Middle Ages were a major influence on scientists during the Renaissance.
Archimedes produced the first known summation of an infinite series with a method that is still used in the area of calculus today.
Archimedes was a famous mathematician whose theorems and philosophies became world known. He gained a reputation in his own time which few other mathematicians of this period achieved. He is considered by most historians of mathematics as one of the greatest mathematicians of all time.
Archimedes was born c. 287 BC in the seaport city of Syracuse, Sicily, which was then a colony of Magna Graecia. The date of his birth is based on an assertion by the Byzantine Greek historian John Tzetzes that he lived for seventy-five years. In The Sand Reckoner Archimedes gives his father's name as Phidias, an astronomer about whom nothing is known. Plutarch wrote that Archimedes was related to King Hieron II, the ruler of Syracuse. A biography of Archimedes was written by his friend Heracleides but this work has been lost, leaving the details of his life obscure. It is unknown, for instance, whether he ever married or had children. Archimedes is believed to have spent part of his youth being educated in Alexandria, Egypt where he was a contemporary of Conon of Samos and Eratosthenes. Some of Archimedes' mathematical works were written in the form of letters to Eratosthenes, who was the chief librarian in Alexandria.
Archimedes died c. 212 BC during the Second Punic War, when Roman forces under General Marcus Claudius Marcellus captured the city of Syracuse after a two year long siege. According to the popular account given by Plutarch in his Parallel Lives , Archimedes was contemplating a mathematical diagram when the city was captured. A Roman soldier commanded him to come and meet General Marcellus but he declined, saying that he had to finish working on the problem. The soldier was enraged by this, and killed Archimedes with his sword. Plutarch also gives a lesser-known account of the death of Archimedes which suggests that he may have been killed while attempting to surrender to a Roman soldier. According to this story, Archimedes was carrying mathematical instruments, and was killed because the soldier thought that they were valuable items. General Marcellus was reportedly angered by the death of Archimedes, as he had ordered him not to be harmed.
The last words attributed to Archimedes are "Do not disturb my circles". This quote is often given in Latin as "Noli turbare circulos meos", but there is no reliable evidence that Archimedes uttered these words, and they do not appear in the account given by Plutarch.
Archimedes' tomb had a carving of his favorite mathematical diagram, which was a sphere inside a cylinder of the same height and diameter. Archimedes had proved that the volume and surface area of the sphere would be two thirds that of the cylinder. In 75 BC, 137 years after his death, the Roman orator Cicero visited the tomb in Syracuse which had become overgrown with scrub. Cicero had the tomb cleaned up, and was able to see the carving and read some of the verses that had been added as an inscription.
The account of the siege of Syracuse given by Polybius in his Universal History was written some seventy years after the death of Archimedes, and was used as a source by Plutarch and Livy. It sheds little light on Archimedes as a person, and focuses on the war machines that he is said to have built in order to defend the city.
Most of the facts about his life come from a biography about the Roman soldier Marcellus written by the Roman biographer Plutarch. According to Plutarch, Archimedes had so low an opinion of the kind of practical invention at which he excelled and to which he owed his contemporary fame that he left no written work on such subjects. While it is true that--apart from a dubious reference to a treatise, On Sphere-Making - all of his known works were of a theoretical character, nevertheless his interest in mechanics deeply influenced his mathematical thinking. Not only did he write works on theoretical mechanics and hydrostatics, but his treatise Method Concerning Mechanical Theorems shows that he used mechanical reasoning as a heuristic device for the discovery of new mathematical theorems.
He was best known for his discovery of the relation between the surface and volume of a sphere and its circumscribing cylinder, for hisformulation of a hydrostatic principle Archimedes' principle and for inventing the Archimedes screw (a device for raising water).
Archimedes Principal states: an object immersed in a fluid experiences a buoyant force that is equal in magnitude to the force of gravity on the displaced fluid.
He also invented things such as the hydraulic screw - for raising water from a lower to a higher level, catapult, the lever, the compound pulley and the burning mirror.
In mechanics Archimedes discovered fundamental theorems concerning the center of gravity of plane figures and solids.
Archimedes probably spent some time in Egypt early in his career, but he resided for most of his life in Syracuse, the principal city-state in Sicily, where he was on intimate terms with its king, Hieron II. Archimedes published his works in the form of correspondence with the principal mathematicians of his time, including the Alexandrian scholars Conon of Samos and Eratosthenes of Cyrene.
He played an important role in the defense of Syracuse against the siege laid by the Romans in 213 BC by constructing war machines so effective that they long delayed the capture of the city. But Syracuse was eventually captured by the Roman general Marcus Claudius Marcellus in the autumn of 212 or spring of 211 BC, and Archimedes was killed in the sack of the city.
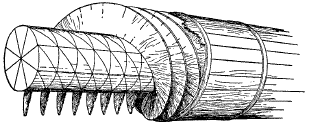
Archimedes Screw, or Archimedean screw, or screwpump, is a machine historically used for transferring water from a low-lying body of water into irrigation ditches. It is one of several inventions and discoveries reputed to have been made by Archimedes, but as some researchers suggest, some form of this mechanism may have been used earlier by Sennacherib, King of Assyria, in the 7th century BC.
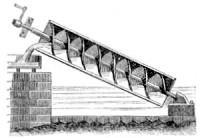
Modern screw pumps, consisting of helices rotating in open inclined troughs, are effective for pumping sewage in wastewater treatment plants. The open troughs and the design of the screws permit the passage of debris without clogging.
Archimedes invented many machines which were used as engines of war. These were particularly effective in the defense of Syracuse when it was attacked by the Romans under the command of Marcellus.

During the Roman siege of Syracuse, he is said to have single-handedly defended the city by constructing lenses to focus the Sun's light on Roman ships and huge cranes to turn them upside down. When the Romans finally broke the siege, Archimedes was killed by a Roman soldier after snapping at him, "Don't disturb my circles,'' a reference to a geometric figure he had outlined on the sand.

While Archimedes did not invent the lever, he gave the first rigorous explanation of the principles involved, which are the transmission of force through a fulcrum and moving the effort applied through a greater distance than the object to be moved.

His Law of the Lever states: Magnitudes are in equilibrium at distances reciprocally proportional to their weights. According to Pappus of Alexandria, his work on levers caused him to remark, "Give me a place to stand on, and I will move the Earth." Plutarch describes how Archimedes designed block and tackle pulley systems, allowing sailors to use the principle of leverage to lift objects that would otherwise have been too heavy to move.
A large part of Archimedes' work in engineering arose from fulfilling the needs of his home city of Syracuse. The Greek writer Athenaeus of Naucratis describes how King Hieron II commissioned Archimedes to design a huge ship, the Syracusia, which could be used for luxury travel, carrying supplies, and as a naval warship. The Syracusia is said to have been the largest ship built in classical antiquity. According to Athenaeus, it was capable of carrying 600 people and contained garden decorations, a gymnasium and a temple dedicated to the goddess Aphrodite. Since a ship of this size would leak a considerable amount of water through the hull, the Archimedes' Screw was said to have been developed in order to remove the bilge water.
Archimedes had stated in a letter to King Hieron that given the force, any given weight might be moved, and even boasted, we are told, relying on the strength of demonstration, that if there were another earth, by going into it he could remove this. Hiero being struck with amazement at this, and entreating him to make good this problem by actual experiment, and show some great weight moved by a small engine, he fixed accordingly upon a ship of burden out of the king's arsenal, which could not be drawn out of the dock without great labor and many men; and, loading her with many passengers and a full freight, sitting himself the while far off, with no great endeavor, but only holding the head of the pulley in his hand and drawing the cords by degrees, he drew the ship in a straight line, as smoothly and evenly as if she had been in the sea.
Archimedes is supposed to have made two "spheres" that Marcellus took back to Rome - one a star globe and the other a device (the details of which are uncertain) for mechanically representing the motions of the Sun, Moon, and planets.
One was a solid sphere on which were engraved or painted the stars and constellations, which Marcellus placed in the Temple of Virtue. Such celestial globes predate Archimedes by several hundred years and Cicero credits the famed geometers Thales and Eudoxos with first constructing them.
The second sphere, which Marcellus kept for himself, was much more ingenious and original. It was a planetarium: a mechanical model which shows the motions of the sun, moon, and planets as viewed from the earth.
Cicero writes that Archimedes must have been "endowed with greater genius that one would imagine it possible for a human being to possess" to be able to build such an unprecedented device.
Many other ancient writers also refer to Archimedes' planetarium in prose and in verse. Several viewed it as proof that the cosmos must have had a divine creator: for just as Archimedes' planetarium required a creator, so then must the cosmos itself have required a creator.
Cicero reverses the argument to contend that since the cosmos had a divine creator, so then must Archimedes be divine to be able to imitate its motions.
The Greek mathematician Pappus of Alexandria, who lived in the fourth century AD, writes that Archimedes wrote a now-lost manuscript entitled On Sphere-making. Pappus also states that it was the only manuscript that Archimedes wrote on "practical" matters. No physical trace of Archimedes' planetarium survives. Cicero refers to it as a "bronze contrivance" while Claudian describes it as "a sphere of glass."
The 1752 engraving of Rowley's orrery suggests how Archimedes' planetarium might have looked. On this orrery the sun, moon and planets revolve along a flat surface driven underneath by a hidden gear works.
Spherical bands surrounding the flat surface represent the celestial equator, the arctic circle, a movable horizon, and the ecliptic marked with the zodiacal signs.
In 1900 a shipwreck discovered off the shore of the Greek island of Antikythera uncovered an unexpected treasure. The ship dated from the first century BC and was sailing from the Greek island of Rhodes. Amidst its cargo was a complicated gear works in a deteriorated state about the size of a cigar box.
The device, now called the Antikythera mechanism, was analyzed by Derek De Solla Price of Yale University, who concluded that it was an ancient planetarium in which the positions of the heavenly bodies were indicated by dials on the face of the device.
The gear works are about as complicated as those in a modern mechanical clock and represent the earliest physical evidence of an advanced metallic mechanism. Price gives evidence that this mechanism was in the Archimedean tradition and strongly suggests that Archimedes' planetarium was its forerunner. A complete presentation of Price's research can be found in Gears from the Greeks.
Although he is often regarded as a designer of mechanical devices, Archimedes also made important contributions to the field of mathematics. Plutarch wrote: "He placed his whole affection and ambition in those purer speculations where there can be no reference to the vulgar needs of life."
Some of his mathematical proofs involve the use of infinitesimals in a way that is similar to modern integral calculus. By assuming a proposition to be true and showing that this would lead to a contradiction, Archimedes was able to give answers to problems to an arbitrary degree of accuracy, while specifying the limits within which the answer lay.
This technique is known as the method of exhaustion, and he employed it to approximate the value of (Pi). He did this by drawing a larger polygon outside a circle, and a smaller polygon inside the circle. As the number of sides of the polygon increases, it becomes a more accurate approximation of a circle. When the polygons had 96 sides each, he calculated the lengths of their sides and showed that the value of � lay between 3 + 1/7 (approximately 3.1429) and 3 + 10/71 (approximately 3.1408).
This was a remarkable achievement, since the ancient Greek number system was awkward and used letters rather than the positional notation system used today. He also proved that the area of a circle was equal to Pi multiplied by the square of the radius of the circle.
He used the method of exhaustion to show that the value of the square root of 3 lay between 265/153 (approximately 1.732) and 1351/780 (approximately 1.7320512). The modern value is around 1.7320508076, making this a very accurate estimate.
Another noted mathematical work by Archimedes is The Sand Reckoner. In this work he set out to calculate the number of grains of sand that the universe could contain. In doing so, he challenged the notion that the number of grains of sand was too large to be counted. He wrote: "There are some, King Gelon (Gelon II, son of Hieron II), who think that the number of the sand is infinite in multitude; and I mean by the sand not only that which exists about Syracuse and the rest of Sicily but also that which is found in every region whether inhabited or uninhabited." To solve the problem, Archimedes devised a system of counting based around the myriad. This was a word used to mean infinity, based on the Greek word for uncountable, murious. The word myriad was also used to denote the number 10,000. He proposed a number system using powers of myriad myriads.
Archimedes helped develop the science of geometry. He proved that the area enclosed by a parabola and a straight line is 4/3 multiplied by the area of a triangle with equal base and height.
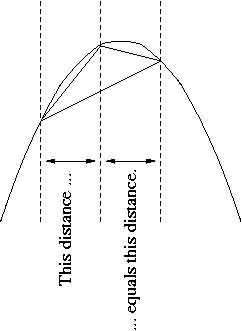
He expressed the solution to the problem as a geometric progression that summed to infinity with the ratio 1/4:
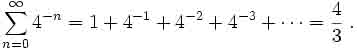
If the first term in this series is the area of the triangle in the illustration then the second is the sum of the areas of two triangles whose bases are the two smaller secant lines in the illustration, and so on. This proof is a variation of the infinite series 1/4 + 1/16 + 1/64 + 1/256 + � � � which sums to 1/3.
It has been suggested that Heron's formula for calculating the area of a triangle from the length of its sides was known to Archimedes. However, the first reliable reference to this formula is given by Heron of Alexandria in the 1st century AD.
His methods anticipated the integral calculus 2,000 years before Newton and Leibniz. Although many solid figures having all kinds of surfaces can be conceived, those which appear to be regularly formed are most deserving of attention. Those include not only the five figures found in the godlike Plato, that is, the tetrahedron and the cube, the octahedron and the dodecahedron, and fifthly the icosahedron, but also the solids, thirteen in number, which were discovered by Archimedes and are contained by equilateral and equiangular, but not similar, polygons.

Truncated Tetrahedron
The first is a figure of eight bases, being contained
by four triangles and four hexagons.

Cuboctahedron
After this come three figures of fourteen bases,
the first contained by eight triangles and six squares
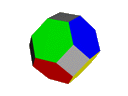
Truncated Octahedron
The second by six squares and eight hexagons,

Truncated Cube
And the third by eight triangles and six octagons.

Rhombicuboctahedron
After these come two figures of twenty-six bases, the
first contained by eight triangles and eighteen squares
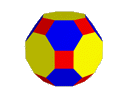
Truncated Cuboctahedron
The second by twelve squares, eight hexagons and six octagons.

Icosidodecahedron
After these come three figures of thirty-two bases, the
first contained by twenty triangles and twelve pentagons

Truncated Icosahedron
the second by twelve pentagons and twenty hexagons,

Truncated Dodecahedron
The third by twenty triangles and twelve decagons.

Snub Cube
After these comes one figure of thirty-eight bases,
being contained by thirty-two triangles and six squares

Rhombicosidodecahedron
After this come two figures of sixty-two bases, the first
contained by twenty triangles, thirty squares and twelve pentagons,

Truncated Icosidodecahedron
The second by thirty squares, twenty hexagons and twelve decagons.

Snub Dodecahedron
After these there comes lastly a figure of ninety-two bases,
which is contained by eighty triangles and twelve pentagons.
Archimedes' work was not as widely recognized in classical antiquity as that of Euclid, and some of his treatises are believed to have been lost when the Library of Alexandria was damaged at various periods in its history. Some of his writings survived through Latin and Arabic translations made during the Middle Ages, and these documents provided Renaissance scholars with an influential source of ideas. Around the year 1586 Galileo Galilei invented a hydrostatic balance for weighing metals in air and water after apparently being inspired by the work of Archimedes.
The most important document containing Archimedes' work is the Archimedes Palimpsest. A palimpsest is a document written on vellum that has been re-used by scraping off the ink of an older text and writing new text in its place. This was often done in the Middle Ages since animal skin parchments were expensive.
In 1906, the Danish professor Johan Ludvig Heiberg realized that a goatskin parchment containing prayers written in the 13th century AD also carried an older work written in the 10th century AD, which he identified as previously unknown copies of works by Archimedes. The parchment spent many years in a monastery library in Constantinople before being sold to a private collector, and reappeared at an auction at Christie's in London in October 1998 where it was sold to an anonymous buyer for $2 million.
The palimpsest contains seven treatises, including the only surviving copy of On Floating Bodies in the original Greek. Most importantly, it contains the only known source of the Method of Mechanical Theorems and Stomachion, which had previously been thought lost. The palimpsest is now stored at the Walters Art Museum in Baltimore, Maryland, where it has been subjected to a range of modern tests including the use of ultraviolet and x-ray light to read the overwritten text.
The treatises contained in the Archimedes Palimpsest are:
- On the Equilibrium of Planes (2 volumes)
This treatise explains the Law of the Lever, and uses it to calculate the areas and centers of gravity of various geometric figures including triangles, paraboloids, and hemispheres. - On Spirals
In this treatise he defines what is now called the Archimedean Spiral. This is an early example of a mechanical curve (a curve traced by a moving point) considered by a Greek mathematician. - On the Sphere and the Cylinder
In this treatise, Archimedes obtains the result of which he was most proud, namely the relationship between a sphere and a circumscribed cylinder of the same height and diameter. He proves that the sphere will have exactly two thirds of the volume and area of the cylinder. A carving of this proof was used on his tomb. - On Conoids and Spheroids
In this treatise Archimedes calculates the areas and volumes of sections of cones, spheres, and paraboloids. - On Floating Bodies (2 volumes)
In the first part of this treatise, Archimedes spells out the law of equilibrium of fluids, and proves that water will adopt a spherical form around a center of gravity. This was probably an attempt at explaining the observation made by Greek astronomers that the Earth is round. His fluids are not self-gravitating, since he assumes the existence of a point towards which all things fall in order to derive the spherical shape.In the second part, he calculates the equilibrium positions of sections of paraboloids. This was probably an idealization of the shapes of ships' hulls. Some of his sections float with the base under water and the summit above water, similar to the way that icebergs float.
- The Quadrature of the Parabola
In this treatise he proves that the area enclosed by a parabola and a straight line is 4/3 multiplied by the area of a triangle with equal base and height. He achieves this by calculating the value of a geometric progression that sums to infinity with the ratio 1/4. - Stomachion
This is a Greek puzzle similar to a Tangram, and the treatise describing it was found in more complete form in the Archimedes Palimpsest. Archimedes calculates the areas of the various pieces. Recent discoveries indicate that Archimedes was attempting to determine how many ways the strips of paper could be assembled into the shape of a square. This is an early use of combinatorics to solve a problem. - Archimedes' Cattle Problem Archimedes wrote a letter to the scholars in the Library of Alexandria, who had apparently questioned the importance of his work. He challenges them to count the numbers of cattle in the Herd of the Sun by solving a number of simultaneous Diophantine equations. There is a more difficult version of the problem in which some of the answers are required to be square numbers. This version of the problem was first solved by a computer in 1965, and the answer is a very large number.
The Sand Reckoner
In this treatise, Archimedes counts the number of grains of sand that will fit inside the universe. This book mentions Aristarchus of Samos' theory of the solar system (concluding that "this is impossible"), contemporary ideas about the size of the Earth and the distance between various celestial bodies. By using a system of numbers based on powers of the myriad, Archimedes concludes that the number of grains of sand required to fill the universe in modern notation. The introductory letter contains the information that Archimedes' father was an astronomer named Phidias. - The Method of Mechanical Theorems
This treatise was thought lost until the discovery of the Archimedes Palimpsest in 1906. In this work Archimedes uses infinitesimals, and shows how breaking up a figure into an infinite number of infinitely small parts can be used to determine its area or volume. Archimedes may have considered this method lacking in formal rigor, so he also used the method of exhaustion to derive the results
Legend has it that Archimedes discovered his famous theory of buoyancy (Archimedes Principle) while taking a bath. He was so excited that he ran naked through the streets of Syracuse shouting "Eureka, eureka (I have found it)!".
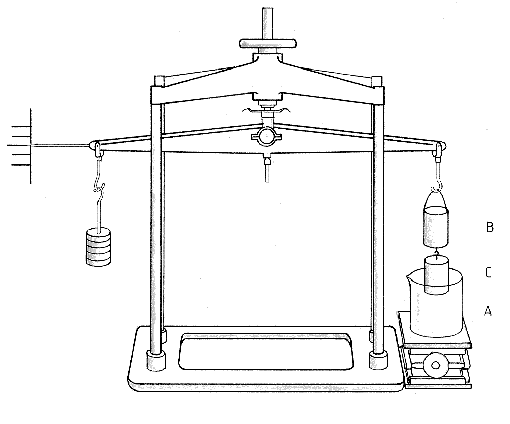
Another legend describes how Archimedes uncovered a fraud against King Hieron II of Syracuse using his principle of buoyancy. The king suspected that a solid gold crown he ordered was partly made of silver. Archimedes first took two equal weights of gold and silver and compared their weights when immersed in water. Next he compared the weights of the crown and a pure silver crown of identical dimensions when each was immersed in water. The difference between these two comparisons revealed that the crown was not solid gold.
Archimedes was killed in 212 BC during the capture of Syracuse by the Romans in the Second Punic War after all his efforts to keep the Romans at bay with his machines of war had failed. Plutarch recounts three versions of the story of his killing which had come down to him.
The first version:
- "Archimedes ... was ..., as fate would have it, intent upon working out some problem by a diagram, and having fixed his mind alike and his eyes upon the subject of his speculation, he never noticed the incursion of the Romans, nor that the city was taken. In this transport of study and contemplation, a soldier, unexpectedly coming up to him, commanded him to follow to Marcellus; which he declining to do before he had worked out his problem to a demonstration, the soldier, enraged, drew his sword and ran him through."
The second version:
- "A Roman soldier, running upon him with a drawn sword, offered to kill him; and that Archimedes, looking back, earnestly besought him to hold his hand a little while, that he might not leave what he was then at work upon inconclusive and imperfect; but the soldier, nothing moved by his entreaty, instantly killed him."
The third version that Plutarch had heard:
- "As Archimedes was carrying to Marcellus mathematical instruments, dials, spheres, and angles, by which the magnitude of the sun might be measured to the sight, some soldiers seeing him, and thinking that he carried gold in a vessel, slew him."
Archimedes was buried Syracuse, where he was born, were he grew up, where he worked, and where he died.
On his grave their is an inscription of pi, his most famous discovery. They also placed on his tombstone the figure of a sphere inscribed inside a cylinder and the 2:3 ratio of the volumes between them, the solution to the problem he considered his greatest achievement.

His nicknames included "the wise one", "the master", and "the great geometer."
No comments:
Post a Comment